Lineární regrese - gradientní sestup
A) Zadání
Pro zadanou vstupní množinu dat (x,y), reprezentující naměřené hodnoty
lineární funkce y=f(x), implementujte učení modelu lineární regrese
optimalizační iterativní metodou gradientního sestupu.
- Parametry úlohy jsou následující:
- vstupní množina dat DataEX08.txt obsahuje jednu nezávisle (x) a jednu závisle (y) proměnnou (pro ilustraci: nezávisle proměnná x představuje počty obyvatel různých měst (v desítkách tis.) a závisle proměnná y pak zisk z obchodní činnosti v těchto městech, tj. počet řádků datasetu=počet měst)
- očekávaná závislost mezi počtem obyvatel města x a ziskem z obchodní činnosti y je určena lineárním modelem (hypotézou) h, přičemž theta značí parametry modelu, jež budou následně optimalizovány:
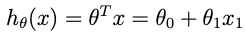
- kvalitu modelu h s konkrétními parametry theta určuje nákladová funkce J(theta), která kvantifikuje chybu modelu výpočtem rozdílu mezi aktuální predikcí h(x) a ground truth y (výstupem J(theta) je tedy skalár):
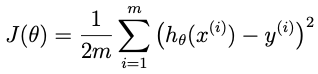
- gradientní sestup je optimalizační metoda pro nalezení vektoru parametrů theta modelu h, která iterativně aktualizuje hodnoty theta modelu h (upravuje hodnoty parametrů theta v opačném směru, než v jakém aktuálně nastavený model klasifikuje – buďto celkově podhodnocuje nebo nadhodnocuje), přičemž rychlost konvergence je řízena parametrem alpha (learning rate):
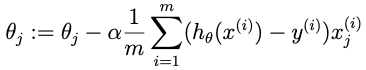
- Poznámky k implementaci:
- nákladovou funkci J(theta) sestavte jako vlastní funkci (m-file) s hlavičkou CostFcn(x,y,theta)
- funkci gradientního sestupu upravující theta(n+1) ← theta(n) sestavte jako vlastní funkci (m-file) s hlavičkou GradDescentFcn(x,y,theta,iterations, alpha), kde iterations značí určený celkový počet iterací výpočtu
- hodnoty iterations a alpha stanovte heuristicky tak, abyste dosáhli optimální (nejrychlejší) konvergence algoritmu
- metoda je iterativní s předem určeným počtem iterací, v každé iteraci si pak ukládejte hodnotu nákladové funkce Cost(n) pro pozdější zobrazení grafu nákladové funkce viz bod 3
- funkce GradDescentFcn bude rámcově obsahovat tyto bloky:
- for iterations {
- Error = …
- update theta(n+1) = …
- Cost(n+1) = …
- }
- Při odevzdání úlohy prezentujte:
- implementace funkcí CostFcn a GradDescentFcn
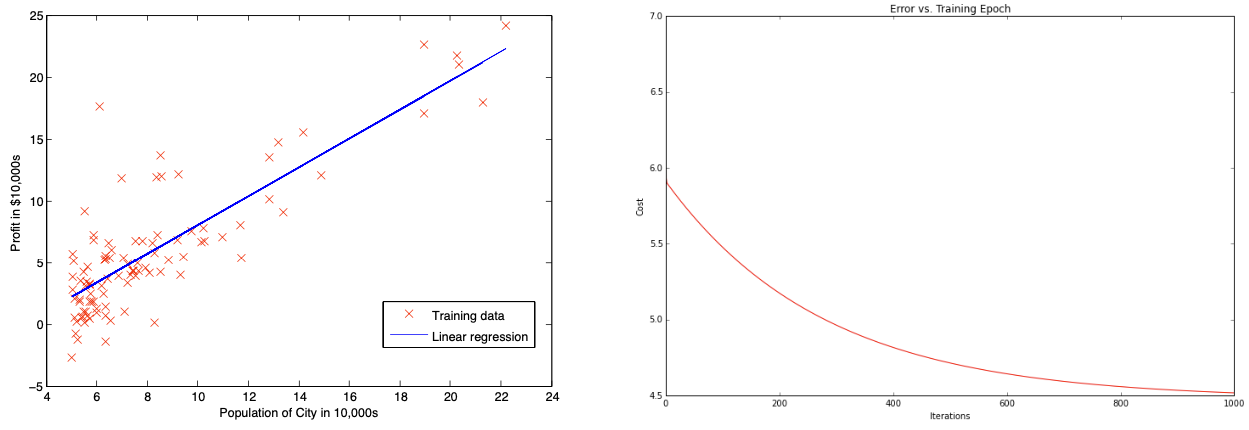
- graf vstupní množiny dat s doplněným lineárním modelem, tj. ScatterPlot(x) doplněný o úsečku reprezentující výsledný model
- graf hodnoty nákladové funkce CostFcn v závislosti na iteraci a popište, jakou vlastnost tato funkce musí vždy nutně mít (viz konvexní optimalizační úloha)
- jaké hodnoty parametrů iterations a alpha a jakým způsobem jste nastavili?
- Extra otázky – nepovinné k zamyšlení:
- Co by bylo třeba učinit pro rozšíření metody na tzv. multivariate tj. pro použití s více nezávisle proměnnými např. x1, x2, …, xn?
B) Info
Metoda gradientního sestupu – stručné opakování v tomto materiálu
Ilustrace vizualizace výsledků – ScatterPlot výsledného modelu
(optimum) a Graf nákladové funkce: