Binární rozhodovací strom – genetický algoritmus
A) Zadání
Zkonstruujte binární rozhodovací strom pro stejnou vstupní funkci jako
v jednom z předchozích cvičení binárního klasifikátoru s tím
rozdílem, že pro určení množiny dělicích atributů v jednotlivých
uzlech stromu použijete namísto výpočtu informačního zisku genetický
algoritmus (GA).
- Binární strom tedy musí modelovat funkční závislost y=f(x) danou tabulkou pod textem:
- Vstupní atributy jsou {x1, x2, x3, x4}.
- Výstupní klasifikační atribut tvoří funkce y(x), jejíž hodnoty do tabulky doplňte rozkladem vašeho student ID v binární soustavě, přičemž vzhledem k počtu řádků tabulky použijte pouze 16 posledních bitů (v horním řádku tabulky je MSB, v dolním pak LSB).
- V tomto cvičení má rozhodovací strom pevnou strukturu podle následujícího schématu – čísla značí index uzlu:
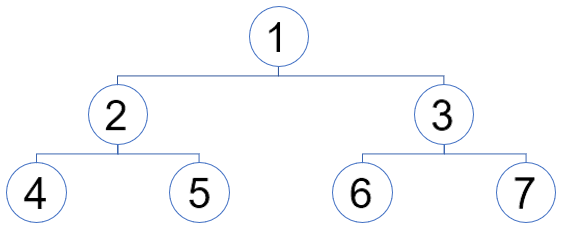
- Konstrukci stromu proveďte pomocí genetického křížení, tj. určením suboptimální množiny J atributů {x1, x2, x3, x4}, přičemž |J|=7 a parametry genetického algoritmu jsou:
- Jedinec populace je definován jako množina J sedmi atributů:
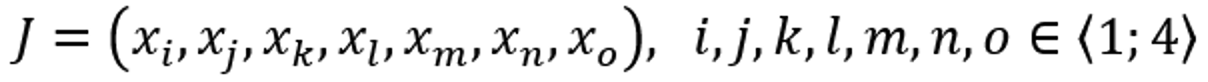
- Počáteční populace čítá N=100 jedinců J1, J2, …, J100 s náhodně vygenerovanými hodnotami z množiny {x1, x2, x3, x4} s rovnoměrným rozložením.
- GA generuje postupně 10 generací vždy se stejným počtem N nových jedinců tak, že křížením dvou po sobě jdoucích rodičů Jk a Jk+1 generace n vzniknou dva noví po sobě jdoucí potomci Jk a Jk+1 v generaci n+1.
- Křížení proveďte metodou simple-crossover v náhodně zvoleném místě množiny (jedince) J, tj. v jedné ze šesti přípustných pozic mezi prvky množiny, která je vždy pro všechna křížení v jedné generaci stejná, mezi generacemi se ale náhodně mění.
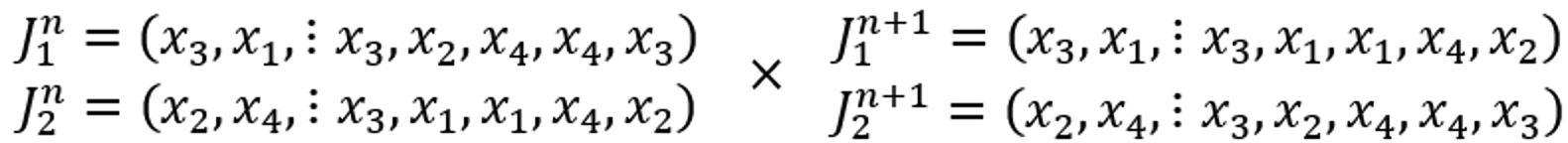
- Jako účelovou funkci (fitness function) pro hodnocení kvality jedince použijte v dřívější úloze definovanou hodnotu klasifikační chyby MisclassRatio.
- Selekce ani mutace se neuplatňuje, do další generace postupuje vždy všech N nově generovaných potomků bez ohledu na fitness rodičů.
- Prezentujte následující výsledky:
- Rozhodovací strom s doplněnými dělicími atributy a uvedenými počty klasifikovaných vzorků v jednotlivých listech stromu pro nejlepší nalezené suboptimální řešení.
- Uveďte, jaký je počet všech přípustných jedinců (tj. kombinací s opakováním) a jaké procento jedinců z toho bylo v úloze použito GA.
- Uveďte v řadě neseřazené hodnoty účelové funkce nejlepších jedinců z každé generace, tj. 10 hodnot. V které generaci se nachází suboptimální jedinec, proč nutně ne v poslední a kdy by tomu tak bylo?
- Uveďte, zda nejlepší řešení GA je méně, stejně nebo více suboptimální, než řešení metodou informačního zisku a výsledek zdůvodněte.
B) Info
Tabulka funkční závislosti y=f(x):
| x1 | x2 | x3 | x4 | y(x) |
| 0 | 0 | 0 | 0 | MSB(ID_16) |
| 0 | 0 | 0 | 1 | … |
| 0 | 0 | 1 | 0 | … |
| 0 | 0 | 1 | 1 | … |
| 0 | 1 | 0 | 0 | … |
| 0 | 1 | 0 | 1 | … |
| 0 | 1 | 1 | 0 | … |
| 0 | 1 | 1 | 1 | … |
| 1 | 0 | 0 | 0 | … |
| 1 | 0 | 0 | 1 | … |
| 1 | 0 | 1 | 0 | … |
| 1 | 0 | 1 | 1 | … |
| 1 | 1 | 0 | 0 | … |
| 1 | 1 | 0 | 1 | … |
| 1 | 1 | 1 | 0 | … |
| 1 | 1 | 1 | 1 | LSB(ID_16) |
