A) Zadání

1. V prostředí Matlab napište skript realizující úlohu shlukové analýzy nehierarchickou metodou k-means ve dvourozměrném prostoru x=(x1,x2), a to pro k=3.

2. Vstupní data x generujte jako náhodná čísla s normálním (Gaussovským) rozložením takto:

   • Vstupní data tvoří 300 vzorků s atributy x1 a x2, přičemž vždy skupina 100 po sobě následujících vzorků odpovídá jednotlivým shlukům (skrytá příslušnost).
   

   • Střední hodnoty shluků jsou [1 1;2 1;x1(3) x2(3)] a odpovídající směrodatné odchylky [1 1;1 1;2 1]; dvojici hodnot [x1(3) x2(3)] navrhněte tak, aby středy shluků tvořily v rovině x rovnostranný trojúhelník.

   • Pro zajištění unikátnosti datové sady použijte inicializaci generátoru náhodných čísel (funkce rng) semínkem o hodnotě vaše VUT ID – s tímto ID bude výsledek skriptu strojově kontrolován při hodnocení, proto generujte nejdříve všechny hodnoty atributu x1 a poté všechny hodnoty atributu x2.
   

3. Implementujte metodu k-means pro generovaná data takto:

   • Před iterativním výpočtem náhodně generovaná vstupní data z předchozího kroku normalizujte lineární funkcí do intervalu <0;1> pro oba atributy x1 i x2:
   

   

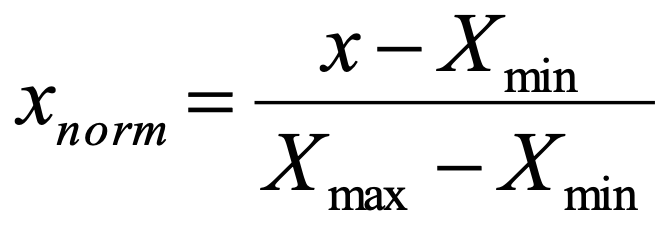
   • Inicializaci středů µ proveďte sesouhlasením s prvními k vzorky vstupních dat z x.
   

   • V iterativním algoritmu k-means použijte jako metriku vzdálenosti Euklidovskou normu L2 (funkce norm):

   

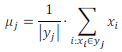
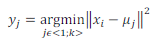
   • Do workspace vypisujte po každé iteraci aktuální hodnotu chybové funkce J (střední kvadratická odchylka x od µ):

   

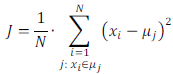
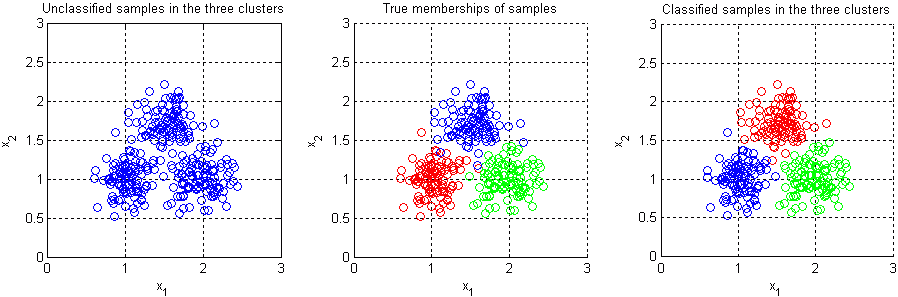
4. Výsledky vizualizujte třemi grafy v jednom okně (funkce subplot) tak, že v levém grafu budou zobrazena neklasifikovaná vstupní data s původními rozsahy, v prostředním grafu skutečná a v pravém grafu klasifikovaná příslušnost vzorků ke shlukům indikovaná barvou a v normalizovaných souřadnicích.

B) Info

Ilustrace vizualizace výsledků shlukové analýzy (pozor, zde neproběhla lineární normalizace a směrodatné odchylky shluků jsou shodné 0.2 viz rozsahy os a rozložení bodů):